算法基础回顾
认识复杂度和简单排序算法
时间复杂度:一个算法常数操作的次数
(额外)空间复杂度:一个算法执行需要额外开辟的内存空间
简单排序算法:O(N^2^)
插入排序:像扑克牌理牌一样
1
2
3
4
5
6
7
8
9
10
11
12
13for (int i=1; i<n; i++) { // 只有一张牌不用排,所以从1开始
int temp = arr[i]; // 记录当前要插入的牌
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j > 0 && temp < arr[j]) { // 往前找当前牌要插入的位置
arr[j] = arr[j-1]; // 找到一次往后挪一次
j--;
}
// j就是当前牌应该插入的位置
if (i != j) {
arr[j] = temp;
}
}选择排序:从右边未排序的元素中选出最小的放在左边
1
2
3
4
5
6
7
8
9for (int i=0; i<n; i++) {
int temp = i;
for (int j=i+1 ; j<n; j++) { // 选出右边最小的
if(arr[temp] > arr[j]) {
temp = j
}
}
swap(arr[i], arr[temp]); // 放在左边
}冒泡排序:从左到右依次把最大的浮到右边
1
2
3
4
5
6
7for (int i=0; i<n ;i++) {
for (int j=0; j<n-i-1; j++) {
if (arr[j] > arr[j+1]) {
swap(arr[j], arr[j+1]);
}
}
}
认识O(NlogN)的排序
master公式
T(N) = a * T(N/b) + O(N^d)
- log
ba < d,时间复杂度:O(N^d^) - log
ba > d,时间复杂度:O(N^log(b,a)^) - log
ba = d,时间复杂度:O(N^d^ * logN)
O(NlogN)排序
归并排序
先排左半部分,再排右半部分,然后把两个有序数组
合并1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27void process(int[] arr, int L, int R) {
if (L == R) return; // 递归终止条件
int M = L + (R-L)>2; // 取中点
process(arr, L, M); // 处理左半部分
process(arr, M+1, R); // 处理右半部分
merge(arr, L, R); // 归并
}
void merge(int[] arr, int L, int R) {
int n = R-L-1;
int[] help = new int[n]; // 开辟辅助空间
int i = 0;
int p1 = L;
int p2 = M+1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (int i=0; i<n; i++) { // 拷贝回原数组,注意是从L+i开始
arr[L+i] = help[i];
}
}- 归并排序的衍生问题:小和问题、逆序对问题
快速排序
快排1.0(小于等于区,大于区):O(N^2^)
快排2.0(小于区,等于区,大于区):O(N^2^)
快排3.0(随机选择参考值):O(N * logN)
- 在长期期望下,随机快排算法的时间复杂度为 O(N*logN)。由于每次划分数据都需要记录 =x 数组的下标范围,因此额外的空间复杂度为 O(logN)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35void quickSort(int[] arr, int L, int R) {
if (L < R) {
// 随机从数组中取一个值放在最后一位,作为划分值
swap(arr, L + (int)(Math.random() * (R -L + 1)), R);
int[] p = partition(arr, L, R); // 得到 =区 的边界
quickSort(arr, L, p[0]-1); // <区
quickSort(arr, p[1]+1, R); // >区
}
}
// 默认以arr[R]作为划分值
int[] partition(int[] arr, int L, int R) {
int less = L - 1; // <区 右边界
int more = R; // >区 左边界
while (L < more) { // L表示当前数的位置
if (arr[L] < arr[R]) { // 当前数 < 划分值
// 右扩 <区
// 当前值和 <区 右边界交换
// 当前值右移
swap(arr, ++less, L++);
} else if (arr[L] > arr[R]) { // 当前数 > 划分值
// 左扩 >区
// 当前值和 >区 左边界交换
// 当前值不动(因为要观察新换过来的值)
swap(arr, --more, L);
} else { // 当前数 = 划分值
// 当前值右移
L++;
}
}
// 将 >区 左边界和划分值交换,使得 >区 左边界就是划分值
swap(arr, more, R);
// 返回 =区 的边界
return new int[] { less + 1, more};
}
桶排序以及排序总结
堆结构
1 | // heapsize |
堆排序:O(N * logN)
- 为什么堆化 heapify() 只用 O(n) 就做到了? - 小齐酱的文章 - 知乎
https://zhuanlan.zhihu.com/p/266665145
1 | // 先把整个数组堆化(大根堆) |
小根堆
Java中的优先级队列默认就是小根堆
1 | PriorityQueue<Integer> heap = new PriorityQueue<>(); |
- 注:当题目中不涉及对堆内部指定数据的变化时,可以用黑盒(Java自带的PriorityQueue),否则需要自己手写堆
Java比较器
1 | // 升序 |
桶排序:O(N)
桶排序是一种不基于比较的排序,必须根据数据状况定制,是应用很窄的一路排序算法。
计数排序
1 | // 1. 找出数组中的最大值,定义辅助数组(空间大小为最大值+1); |
- 基数排序(基数就指几进制)
1 | // 先根据个位数排序,再根据十位数排序,再根据百位数排序... |
排序的稳定性
- 排序的稳定性:值相同的元素在排序完之后能否保证原来的
相对次序不变,主要用于有多个排序条件时,希望在完成后一个排序后能够保留前一个排序的结果。 - 可以具有稳定性的排序:冒泡排序(相等的时候不换)、插入排序、归并排序、计数排序、基数排序
- 不具备稳定性的排序:选择排序、快速排序、堆排序
排序总结
| 排序 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 选择排序 | O(N^2^) | O(1) | X |
| 插入排序 | O(N^2^) | O(1) | O |
| 冒泡排序 | O(N^2^) | O(1) | O |
| ==快速排序(随机)== | O(N * logN) | O(logN) | X |
| 归并排序 | O(N * logN) | O(N) | O |
| 堆排序 | O(N * logN) | O(1) | X |
- 目前来说,基于比较的排序,其时间复杂度不会在O(N * logN)以下
- 目前来说,时间复杂度为O(N * logN)、空间复杂度为O(1),并且可以保持稳定的基于比较的算法不存在
- 当你需要排序的样本数量小于60,直接选择插入排序, 虽然插入排序的时间复杂度为O(N²), 但在基数60以内,插入排序的时间复杂度为O(N²)的劣势体现不出来, 反而由于其常数项很低,在小样本情况下,插入排序极快。
链表
哈希表(HashSet、HashMap)
- HashSet只有key、HashMap有key还有伴随数据value
- 放入哈希表的东西,如果是基础类型,内部按值传递,内存占用就是Key值本身的大小
- 放入哈希表的东西,如果不是基础类型,内部按引用传递,内存占用就是Key值内存地址的大小
有序表(TreeSet、TreeMap)
- 要求Key是可以比较的
- 放入有序表的东西,如果是基础类型,内部按值传递,内存占用就是Key值本身的大小
- 放入有序表的东西,如果不是基础类型,==必须提供比较器==,内部按引用传递,内存占用就是Key值内存地址的大小
单链表
做题的时候要做笔试和面试两种情况!
1. 判断一个链表是不是回文链表
- 直接全部放到栈里
- 只把右半部分放到栈里去:==快慢指针==(CODING!!!)
- 快指针一次走两步,慢指针一次走一步,快指针走到尽头的时候,慢指针位于中点,注意:
- 总元素个数为奇数、偶数时,对慢指针停止位置的要求
- 空间复杂度O(1):改链表
- 快慢指针,慢指针走到中点后,让右半部分逆序,然后记住左右半部分各自的链表头,分别向前遍历比对,返回True/False之前需要把链表还原
2. 把一个链表中的元素根据某个值,分成小于区,等于区大于区,大于区
- 笔试:放到数组中进行partition,然后再串回链表;
- 面试:创建6个变量:SH、ST、EH、ET、BH、BT
3. 找到两个链表相交的第一个节点
- 判断一个链表有没有环,如果有环,找到其入环节点
- 使用HashSet,第一个重复的节点就是入环节点,如果没有重复节点并且走到头了,就没有环
- 使用快慢指针,如果有环,快慢指针一定会相遇,在第一次相遇之后,快指针指向head节点,慢指针不动,快慢指针开始前进,每次都只前进一步,两个指针再次相遇的节点就是入环节点
- 根据两个链表的入环节点,找到第一个相交节点
- 两个无环单链表(
loop1 == null且loop2 == null):如果相交,从相交节点开始到最后都是公共部分,第一个相交节点根据两个链表长度计算 - 一个有环、一个无环(
loop1和loop2有一个不为空):不会相交 - 两个都有环(
loop1 != null且loop2 != null)- 完全独立(loop继续往下走,回到自己之前遇不到loop2)
- 共用环、入环节点一样(
loop1 == loop2):同两个无环单链表 - 共用环、入环节点不一样(loop继续往下走,回到自己之前能遇到loop2)
- 两个无环单链表(
二叉树
遍历二叉树
1. 递归遍历
递归序:每个节点可以访问三次
1 | public static void f(Node head) { |
- 先序:头、左、右(第一次来到一个节点打印)
- 中序:左、头、右(第二次打印)
- 后序:左、右、头(第三次打印)
2. 非递归遍历:栈
先序(先把头节点压到栈里)
- 从栈中弹出一个节点cur
- 打印cur
- 如果有左右子节点,先==右==节点入栈、后==左==节点入栈
- 重复1~3
后序
使用两个栈(先把头节点压到栈里):
- 从栈中弹出一个节点cur
- 将cur压入收集栈
- 如果有左右子节点,先==左==节点入栈、后==右==节点入栈(这样入收集栈的顺序就是头、右、左)
- 重复1~3
- 将收集栈依次出栈(顺序逆序变为:左、右、头)
使用一个栈:
后序遍历打印一个节点只有两种情况:
- 当前节点是叶子节点
- 当前经过节点的右子节点是上一次访问的节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27public static void posOrderUnRecur2(Node h) {
System.out.print("pos-order: ");
if (h != null) {
Stack<Node> stack = new Stack<Node>();
stack.push(h);
Node c = null;
while (!stack.isEmpty()) {
// h: 上一次打印的元素
// c:当前(栈顶)元素
c = stack.peek();
if (c.left != null && h != c.left && h != c.right) {
// 有左子树,并且不是上一个出栈元素的父节点
stack.push(c.left);
} else if (c.right != null && h != c.right) {
// 有右子树,并且右子树不是上一个出栈的元素
stack.push(c.right);
} else {
// 包含以下几种情况
// 1. 叶子结点
// 2. 有右子树,并且右子树是上一个打印的节点
System.out.print(stack.pop().value + " ");
h = c;
}
}
}
System.out.println();
}
中序:对于每棵树,把它的左孩子全部压入栈中,并依次弹出打印,并对弹出节点的右子树重复
算法题
1. 二叉树的宽度优先遍历(层序遍历)
二叉树的先序遍历就是深度优先遍历
宽度优先遍历:放队列里,先放左后放右
- Java里的Linkedlist就是队列
求一个棵二叉树的宽度,设置如下几个变量
- levelMap:记录每个节点所在层数,在父节点出队列时初始化;
- curLevel:当前所在层数
- curNodeLevel:当前结点所在层数
- max:记录最大宽度
- 记得处理最后一层是最大层的返回值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37public static int getMaxWidth(Node head) {
if (head == null) return 0;
// 设置辅助变量
LinkedList<Node> queue = new LinkedList<>();
queue.add(head);
HashMap<Node, Integer> levelMap = new HashMap<>();
levelMap.put(head, 1);
int curLevel = 1;
int curLevelNodes = 0;
int max = Integer.MIN_VALUE;
Node cur = null;
while (!queue.isEmpty()) {
cur = queue.poll();
int curNodeLevel = levelMap.get(cur);
if (curNodeLevel == curLevel) {
// 如果当前结点还在当前层,当前层结点数++
curLevelNodes++;
} else {
// 如果当前结点是下一层的
// 结算本层宽度
max = Math.max(max, curLevelNodes);
curLevel++;
curLevelNodes = 1;
}
// 将cur子结点入队列
// 并且初始化子结点层数
if (cur.left != null) {
queue.add(cur.left);
levelMap.put(cur.left, curNodeLevel + 1);
}
if (cur.right != null) {
queue.add(cur.right);
levelMap.put(cur.right, curNodeLevel + 1);
}
}
return Math.max(max, curLevelNodes);
}
2. 判断是否是各种二叉树
- 搜索二叉树:每一颗树都是左结点比根结点小,右结点比根结点大:中序遍历升序
- 完全二叉树:要么这棵树是满的,要么不满的是最后一层(左半部分是满的):宽度遍历
- 每个结点,有右无左,返回false
- 在1.不违规的条件下,如果遇到了第一个左右不全的结点(一定是左有右无),后续都必须是叶子节点
- 满二叉树
- 求树的最大深度L和节点个数N,应该满足N = 2^L^-1
- 平衡二叉树:对于任何一个字数来说,左树的高度差和右数的高度差都不超过1
- 左树平衡
- 右树平衡
- | 左树高度 - 右树高度 | <= 1
二叉树的递归套路:解决树形DP(动态规划)
- 列出所有的可能性
- 确定左子树需要提供的信息
- 确定右子树需要提供的信息
- 根据2、3求全集作为递归的返回类型
- 在根结点中
- 先处理空值
- 获得左子树提供的信息
- 获得右子树提供的信息
- 返回根结点需要提供的信息
3. 两个二叉树的最低公共祖先
- 从下往上走最初汇聚的点,存储从某个结点从下往上走的一个链;
- 递归套路(一点点抽象)
4. 找一个结点的后续结点(中序遍历)
前提:树中的每个节点都有一个指向父节点的指针
- 如果当前节点有右子树,那后续节点就是右子树的最左边的节点;
- 如果当前节点 没有右子树,那后续节点是从当前节点往父节点走,直到当前节点是父节点的左子树,此时的父节点就是最初的当前节点的后继节点。
5. 二叉树的序列化和反序列化
关键是理解各种遍历方式,并且活用队列
6. 折纸问题
重点在于每个折痕上边新的折痕都是凹的,下边新的折痕都是凸的
图
图问题的复杂点在于,由于图有多种表示方式,即使是同一种算法,不同的表示方式下的写法也不同
图的表示方法
- 邻接表:记录每个节点和它直接相关的节点
- 邻接矩阵:正方形矩阵,行列都是节点集
一个经典的图结构
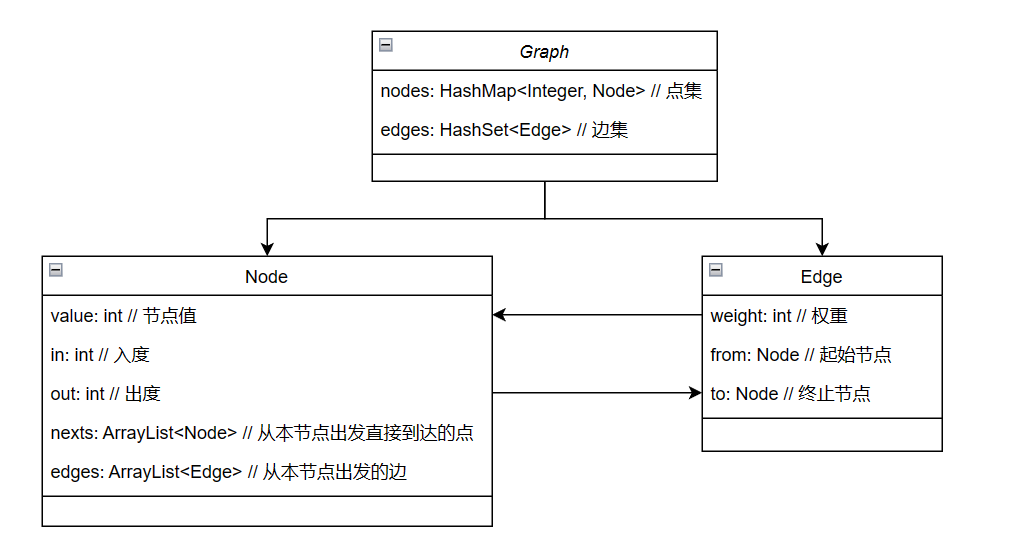
nodes的键值key就是Node的value属性
图的相关算法
图的遍历
宽度优先遍历
宽度优先遍历就是从一个节点开始,先遍历跟他相邻的所有节点,再遍历跟相邻节点相邻的所有节点,依次向外扩散,像水波一样
- 准备一个队列queue
- 准备一个HashSet用来记录是否遍历过当前节点
- 开始先把头节点入队
- 之后每次弹出队尾元素打印之后,如果弹出元素的相邻节点不在HashSet的记录中就入队,并且记录到HashSet,否则不做处理,继续弹出队尾元素循环往复。
深度优先遍历
一条路走到底,走完之后回去走没走过的
换言之,深度遍历的主要是想就是,找出当前顶点第一个未被访问的邻接节点,然后以该节点为新顶点,继续访问下去,直至刚访问过的顶点没有未被访问的邻接点位置,然后返回前一个访问过的仍有未被访问邻接点的顶点,继续访问该顶点的下一个未被访问的邻接点。
- 准备一个栈stack
- 准备一个set
- 先把头节点入栈(这里是进去的时候打印)
- 当stack不为空的时候
- 弹出栈顶元素ele
- 遍历ele的左右邻居
- 如果邻居没有被记录在set中
- ele入栈(为了能够再次返回这个节点访问剩余未被访问的邻接节点)
- 这个邻居也入栈(打印这个邻居)
- 然后
break,结束对所有邻居的这次遍历
- 如果邻居没有被记录在set中
- 重复1~2
拓扑排序(无环有向图)
把有向图中的方向理解为尾节点是头节点的前置,拓扑排序即是找到一个顺序,使得所有节点的前置都在这个节点之前
- 先找到入度为0的节点
- 把该节点对后续节点的影响都去掉:所有
邻居(紧邻的后续节点)的入度都减少1 - 再找下一个入度为0的节点
- 重复1~3
最小生成树(无向图)
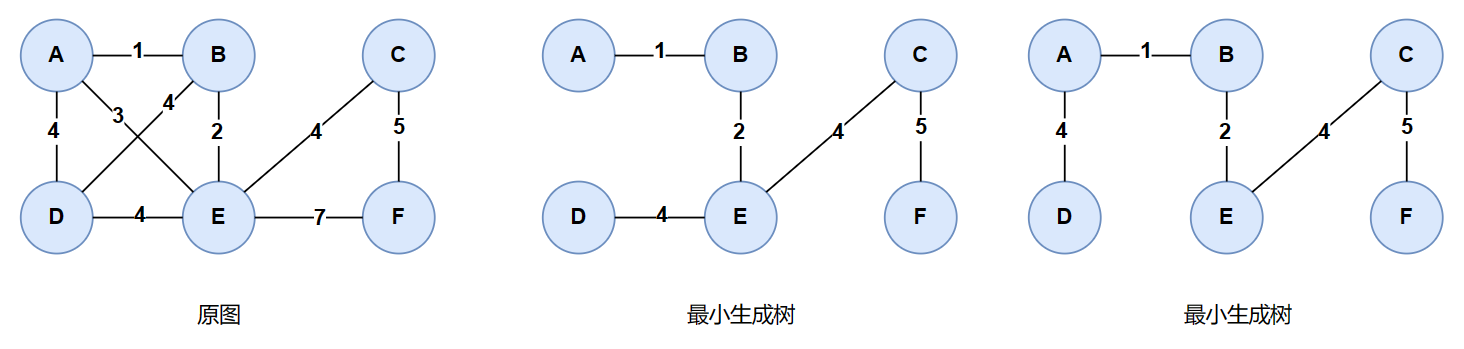
prim
将所有顶点分成两类,A类存放最小生成树中的节点,B类存放剩下的节点,每次都遍历A类所有的节点,找到和B类中节点相连权值最小的节点,并且和A类中的节点不成环,将该节点加入到A类,直至所有的节点都被加入到A类
kruskal
普利姆(Prime)算法是以 点 为基础,挑选与 已有点 相连的最小边。
克鲁斯卡尔(Kruskal)算法是以 边 为基础,先将边从小到大排列,从小到大的添加不构成「环路」的边。
是否构成环路通过
并查集来判断
最短路径
适用范围:没有权值为负数的边
Dijkstra 算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法,时间复杂度 O(n2).
要点
每次从 「未求出最短路径的点」中 取出 距离起点 最小路径的点,以这个点为桥梁 刷新「未求出最短路径的点」的距离。
以这个点为桥梁刷新的意思就是起点通过这个点到达终点和直接到达终点那个距离更短- 参考链接:Dijkstra算法详解 通俗易懂 - 知乎 (zhihu.com)
- 其中,寻找距离起点最小路径的点是通过遍历实现的,可以通过堆来优化,但是不能使用Java提供的堆,因为该算法中的距离在堆中存储时会发生变化,使用Java提供的堆与遍历无异,需要自己根据该算法设计一个专门的堆。
前缀树
前缀树的结构
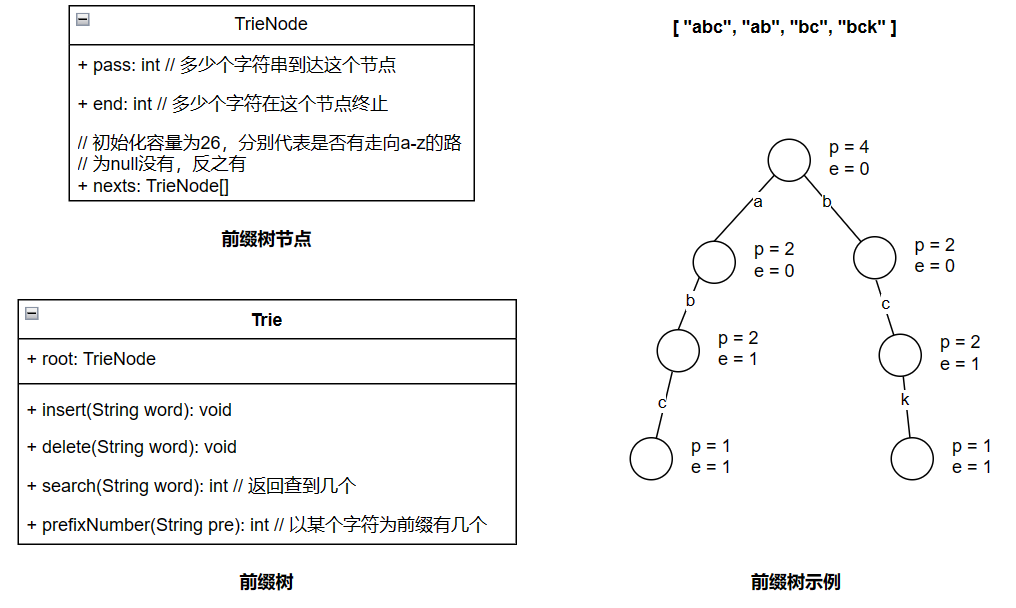
- 根结点:代表数组中有多个字符串以空串为前缀,也就是一共有多个字符串
- 当字符集元素过多时,使用数组来表示nexts会占用较大空间,可以替换为HashMap<Char, Node>,表示通过key表示的字符走到value表示的节点
贪心算法
解题套路
- 实现一个不依靠贪心策略的解法X,可以用最暴力的尝试;
- 脑补出贪心策略A、贪心策略C、贪心策略C……
- 用解法X和对数器,去验证每一个贪心策略,用实验的方式得知哪个贪心策略正确
- 不要去纠结贪心策略的证明
- 找题练、写好对数器模板
N皇后
暴力递归
暴力递归就是尝试
- 把问题转化为规模缩小了的同类问题的子问题;
- 有明确的不需要进行递归的条件(base case);
- 有当得到了子问题的结果之后的决策过程;
- 不记录每一个子问题的解。



